분할정복 vs 다이나믹 프로그래밍
여러 하위 문제로 나누어 먼저 해결한 뒤, 그 결과들을 이용해 큰 문제를 해결하는 기법
| 분할정복 | 다이나믹 프로그래밍 (이하 DP) | |
| 하위 문제 | 중복이 없음 | 중복 있음 즉, 단순 분할정복 수행 시 중복된 작업을 수행 (해결 방법은 아래 이어서) |
| 고려사항 | 시간 - 메모리 간의 trade-off |
DP 구현방법
TODO 두 방식의 차이점 체감하기
| Top Down | Bottom Up | |
| 구현 방법 | 재귀, memoization | for 루프, Tabulation |
[생각해보기] 시간복잡도 (피보나치 수열 vs 팩토리얼 문제)
| 피보나치 수열 | 팩토리얼 | |
| 점화식 | fibo(n) = fibo(n-1) + fibo(n-2) | factorial(n) = n*factorial(n-1) |
| 시간복잡도 | [재귀로 구현 시] O(2^n) 함수를 계속 두번씩 부르기에 트리로 표현하면 [DP로 구현 시] O(N) 중복되는 계산을 줄일 수 있음 |
O(N) |
그 외에도 배낭문제는 N개의 물건에 대한 조합에 대해 Brute Force 한다면 넣고/안넣고 2^N 개의 시간복잡도를 갖게됨. 하지만 DP를 이용해 시간복잡도를 줄일 수 있음. 하지만 처음부터 Tabulation 점화식을 찾기는 어려움.
다음은 내가 이해한 코치님의 조언: iteration으로 구현 후 단계적인 최적화 사고를 했으면
1. 완전탐색
2. 문제를 잘라볼 수 있다면 분할 정복
2-1. sub problem을 호출한다면 재귀
2-2. 중복된 sub problem 이라면 caching (memoization)
2-3. 절반 크기의 sub problem으로 쪼갤 수 있다면 이분 탐색 = 탐색 시간이 O(logN)으로 줄어듦
3. 문제의 유형에서 순서 및 과거의 값 참조를 왔다갔다한다면 queue, stack 자료구조를 사용 (동굴 탐험이라는 표현 ?)
4. 관계가 있다면 graph로 표현 가능
문제로 이해하는 DP 구현 방법
- 코드트리 > 자료구조&알고리즘 > DP 학습 내용을 정리했습니다.
- 백준 DP관련 인기 문제집에서 문제들을 발췌했습니다.
Bottom-Up
| #1463 1로 만들기 |
| - 전형적인 Bottom-Up Approach 접근 - dp[i] = 숫자 i 를 만들기 위한 최소 연산 횟수 |

| subproblem을 그대로 합치면 되는 DP |
| 코드트리 #타일 채우기 (2xN 벽을 2x1, 1x2 타일로 채우기) 백준 #11726 2xN 타일링 (동일) 백준 #1904 01타일 (위 문제와 유사) |
| - 일일이 나열해서 직접 규칙을 찾을 수도 있지만, 수가 많을 경우에는 불가능에 가깝다. 어떻게 하면 문제를 쪼개서 볼 수 있을지 학습할 수 있었다. - sub problem을 찾는게 핵심 - 이때 상수가 제일 고민인데 타일 문제에서 sub problem 에 좌우 붙는 케이스를 고려해 곱하기 2를 해야하나 했지만, 그건 sub problem에서 해결할 일. 곱할 필요 없음 |


| 코드트리 #BST 개수 |
| (가벼운 추측) 가짓수 문제는 누적합, 시그마를 자주 사용하는 것 같다 |

| 격자 안에서 한 칸씩 전진하는 DP |
| - 특정 위치 (r, c)에서의 이동은 (r+1, c) 혹은 (r+1, c+1) 지점으로만 가능 - 점화식은 단순 사칙연산 뿐만 아니라 max 등의 함수로도 표현 가능하다. |
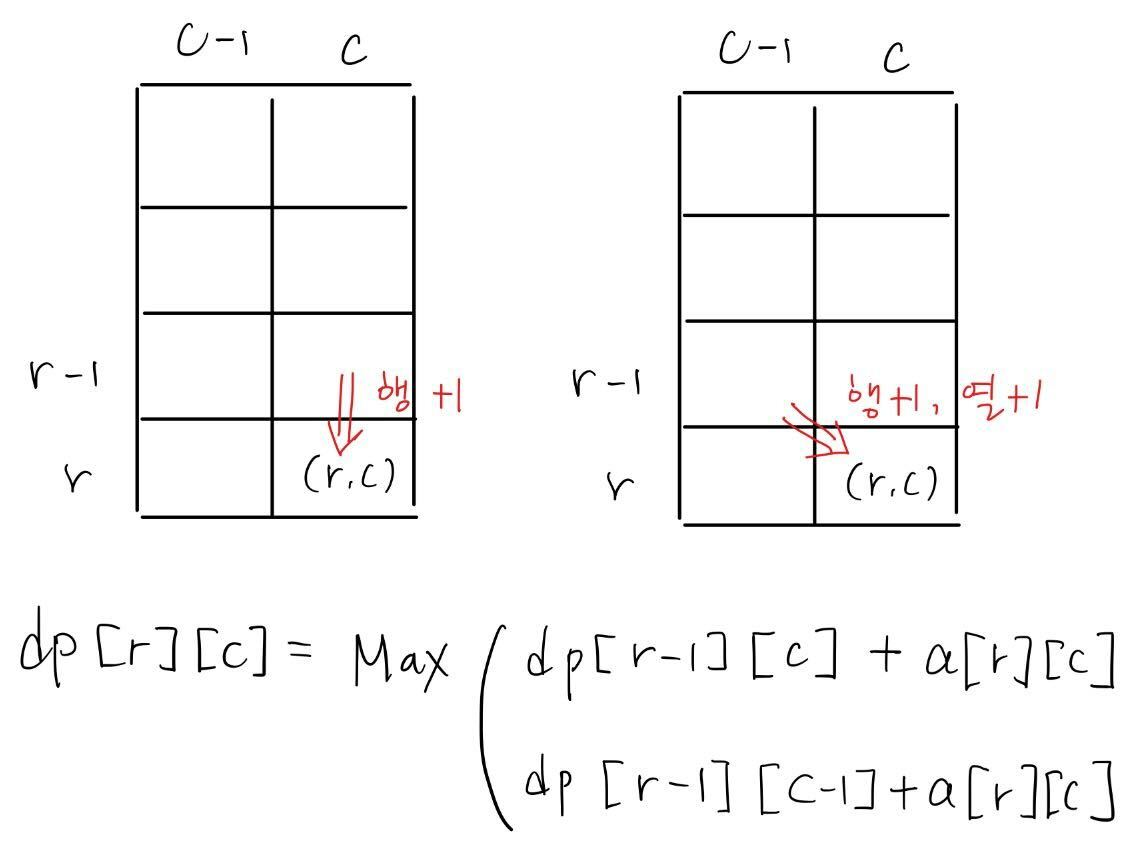
| #2579 계단 오르기 |
| - 점화식이 잘못 설정되면, 틀리게된다. 올바른 점화식인지 어떻게 검증하고 시작할 수 있을까? - 그리고 기저 초기화 및 점화식 범위 외 예외처리 필요함 |

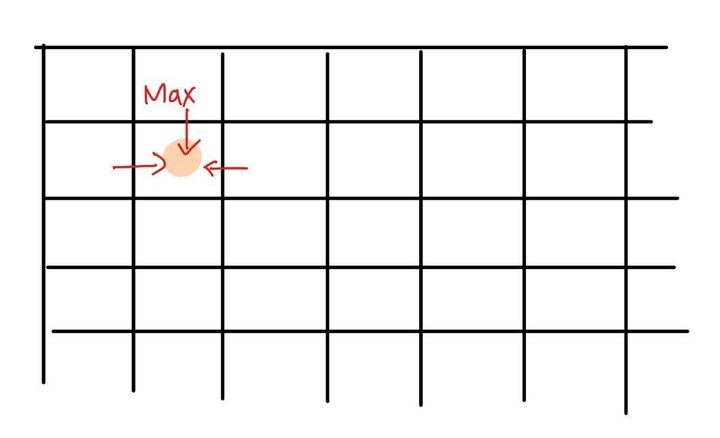
| # 2169 로봇 조종하기 |
| - 격자라 냅다 bfs로 접근할 것 같은데 어쩔때 dp를 써야할까? (과거 값으로 표현이 될 때..?) - 단순 아래/오른쪽 이동만 가능하지 않고, 왼쪽도 가능해서 복잡해진 이유는 뭘까? (이보다 더 심플한 문제는 없을까? 위에거 같긴 한데 백준에서 말야) - TODO: bfs 풀이가 적합하지 않는 이유 |
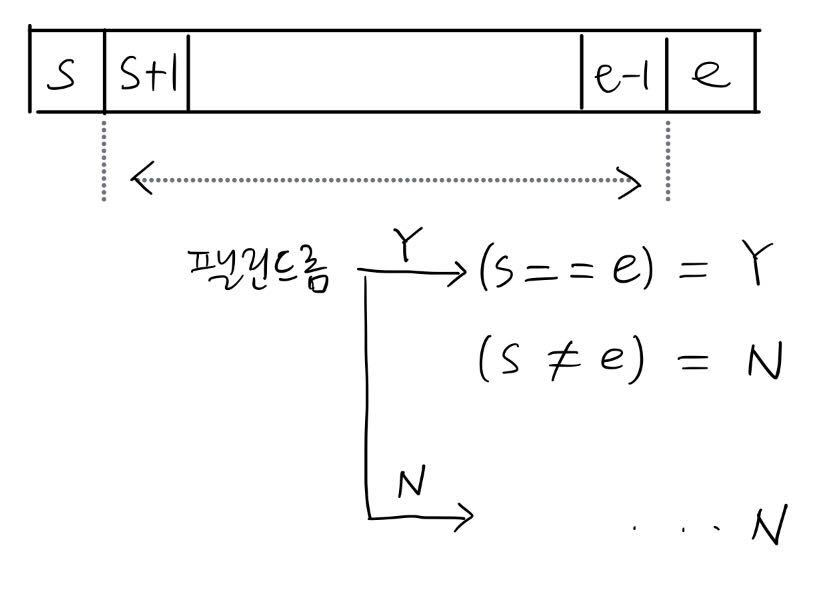
| #10942 팰린드롬 |
| - dp[s][e] = s ~ e 위치의 부분 문자열의 팰린드롬 여부 - 탐색할 범위의 안쪽으로 sub-problem을 좁히는 연습 |
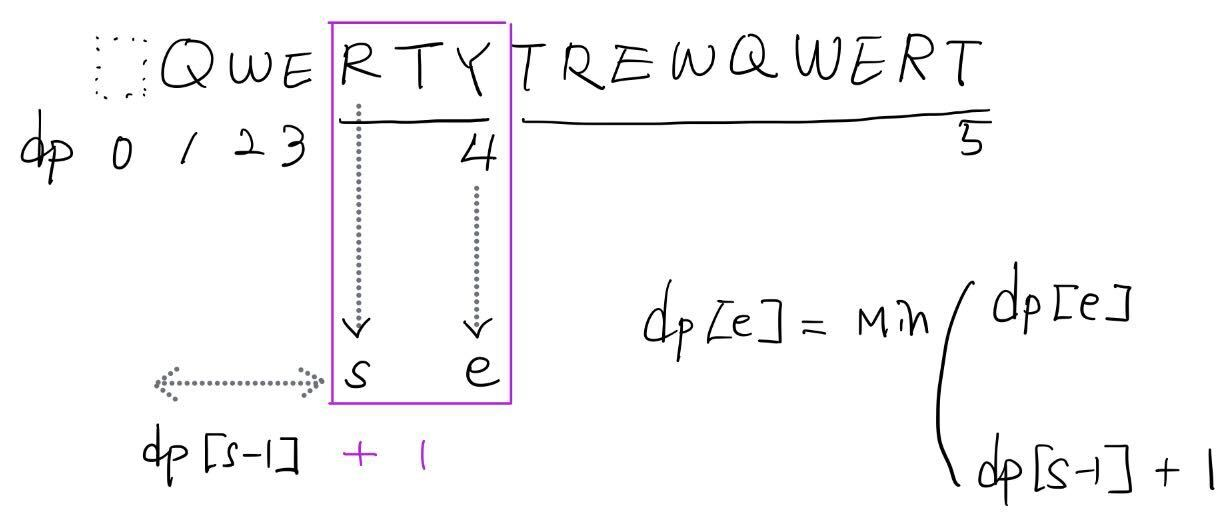
| # 1509 팰린드롬 분할 |
| - 초기화, 순회 영역 설정이 어려움;; |
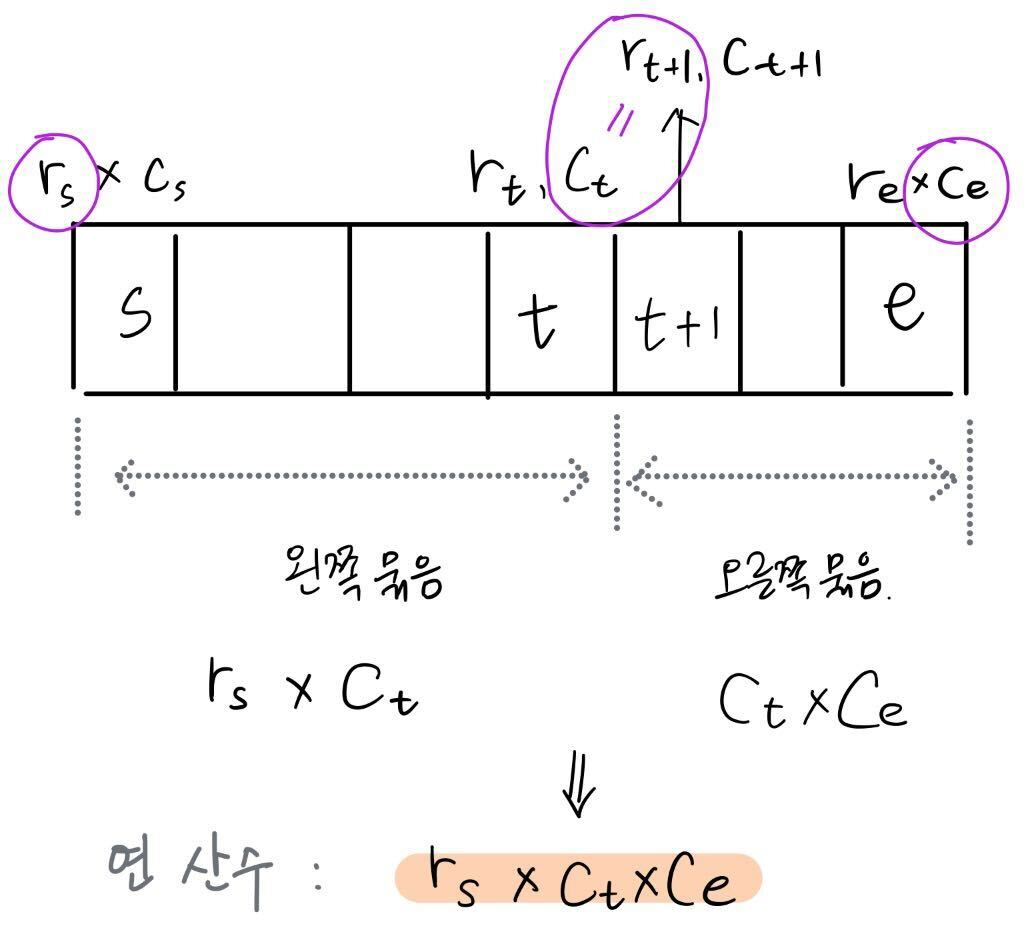
| #11049 행렬 곱셈 순서 | |
| - dp[s][e] = s ~ e 내 최소 연산 수 |
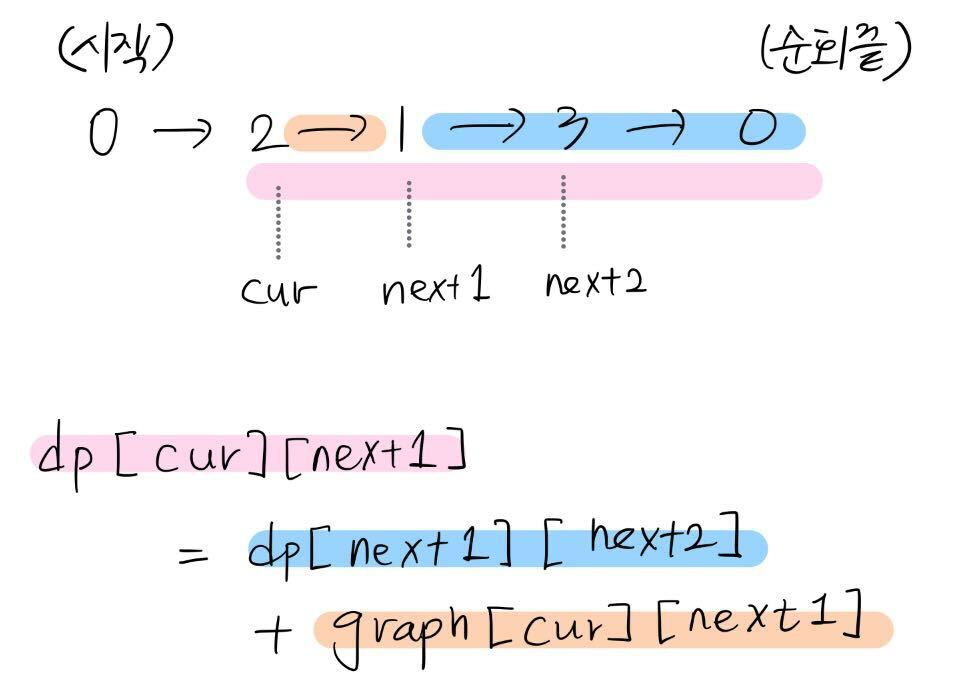
| #2098 외판원 순회 |
| - #10971 외판원 순회 2 와의 차이점 ( N은 증가했으나 시간복잡도, 공간복잡도가 제한적) - 비트마스킹 + DP + DFS |
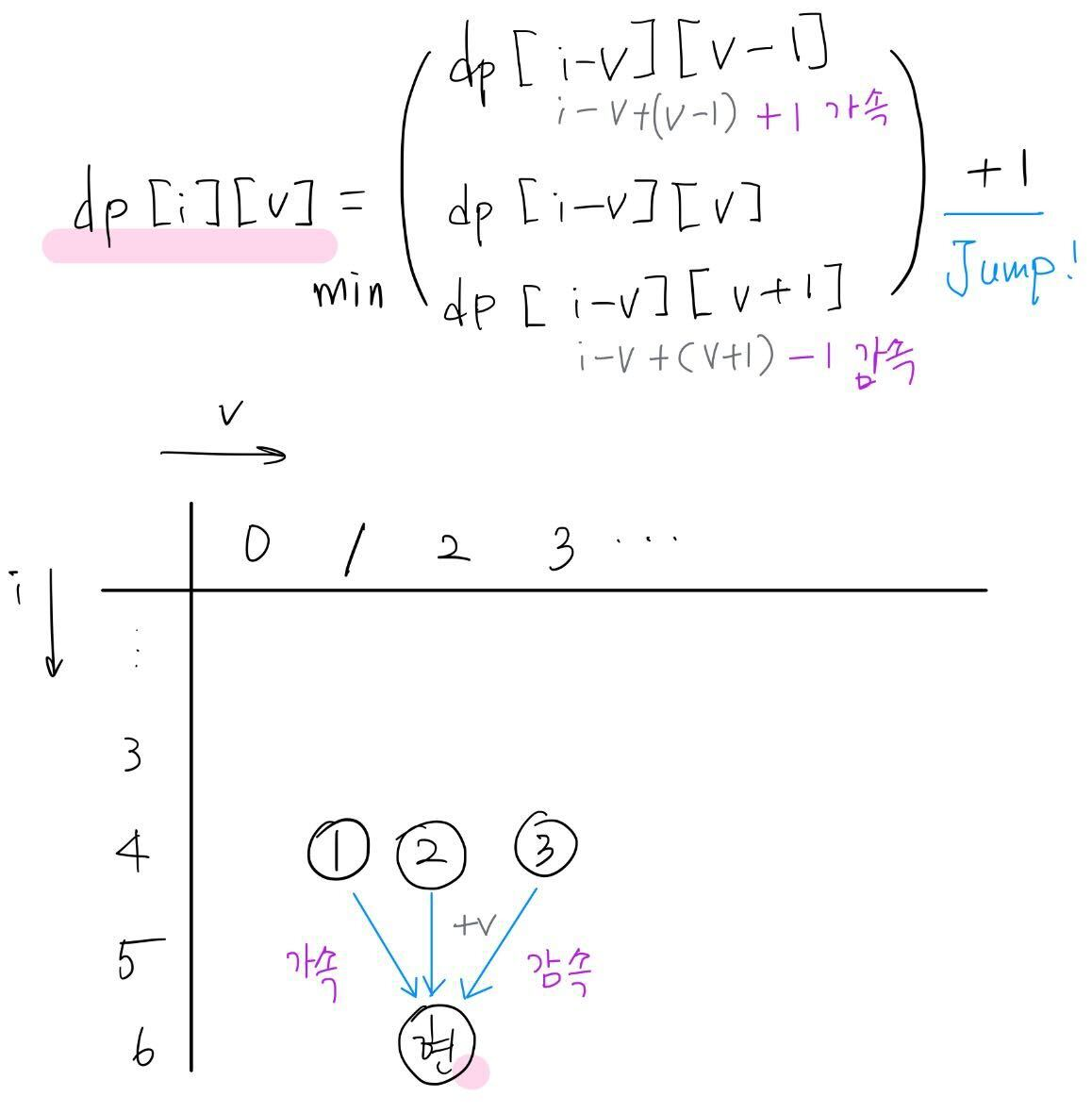
| #2253 점프 |
| - 수학 수학.. 흑.. |

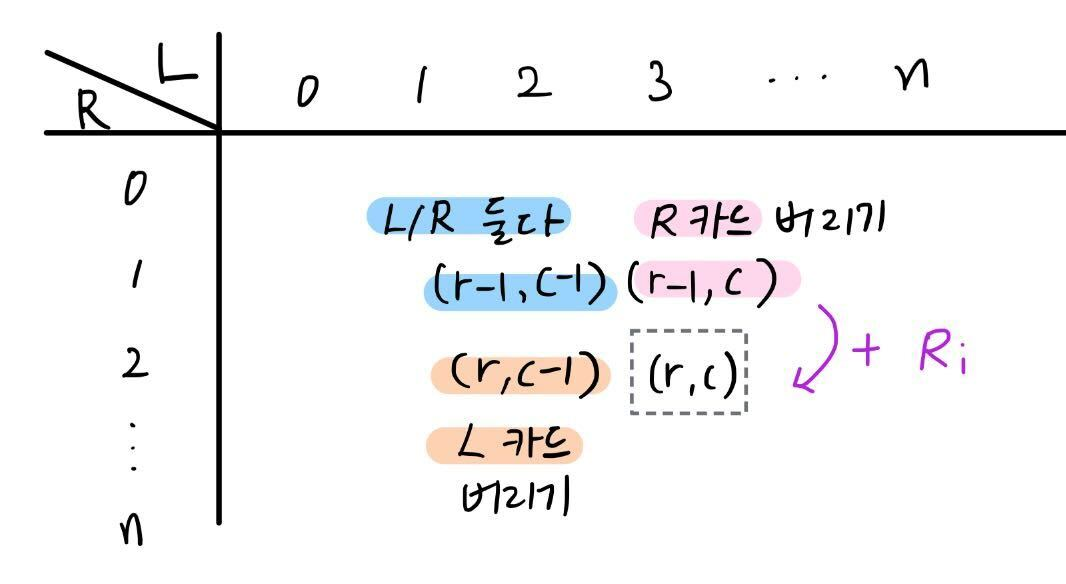
| #10835 카드 게임 |
| if right[col] < left[row]: dp[row][col] = max(dp[row][col-1] + right[col], dp[row-1][col], dp[row-1][col-1]) else: dp[row][col] = max(dp[row-1][col], dp[row-1][col-1]) |
'2️⃣ 개발 지식 B+ > 코딩 테스트' 카테고리의 다른 글
| [python] 코테 유형별 템플릿 모음 (0) | 2024.10.27 |
|---|---|
| [python] 유용한 문법 (0) | 2024.09.07 |
| [백준/python] Greedy 유형 모음집 및 접근 컨셉 (0) | 2024.08.28 |
| [백준/python] DP 유형 - 배낭(Knapsack) 문제 (0) | 2024.08.26 |
| [백준/python] DP 유형 - LIS & LDS 그리고 LCS (0) | 2024.08.26 |



